Lecture 7

Bertrand Competition

古诺模型是在产量上竞争，而伯川是在价格上进行竞争。

players: 两家公司

cost: 固定的边际成本c

strategy： 制定价格$p_1, p_2$，为了简化模型，范围在[0, 1]之间。

$Q(p) = 1-p$表示总的产量， $p = min(p_1, p_2)$。

产量的计算： $q_1 = \left\{\begin{matrix} 1-p_1 & p_1<p_2\\ 0& p_1>p_2\\ (1-p_1)/2& p_1=p_2 \end{matrix}\right.$ 这是两个互为替代品的商品，比如可口可乐或者是百事可乐，只要价格有大小之分，那么就朝一边倒，否则是平分市场分额。

payoffs: $q_1*p_1-c*q_1$

找到玩家1的最佳对策，不进行求导： $\hat q_1 = BR_1(p_2)\left\{\begin{matrix} p_1>p_2 ，& p_2<c, 表示退出市场\\ p_1<p_2，& c<p_2<垄断价格\\ 垄断价格，& p_2>垄断价格\\ p_1\ge c& p_2=c \end{matrix}\right.$ 垄断是会使得公司收益最大，并且总利润也是最大的。

$NE = (p_1=c, p_2=c)$

为什么是这个点，假设初始的点为$(c, c+3\delta )$，当然公司1会改变自己的价格$(c+2\delta, c+3\delta )$，最终肯定还是会收敛到纳什均衡点。

在纳什均衡点的位置，p=c, profit = 0.

能够得到的结论：

1. 即使只有两个公司进行竞争，结果像是完全竞争的结果。
2. 即使像古诺模型那样设置，但是策略集合是不同的。

实际上，商品应该是有差别的(differentiated products)。

homework:

linear city model

election

0 1

|---------------------------------------------------------|

选民在数轴上是均匀分布的

玩家：voters

策略：

1. 你是否要参加。
2. 一旦参加只能投票给最近的人，每一个人都能成为candidate，一旦参与那么不能给自己投票，即不能选择自己的立场
3. 大多数选择的candidate成为赢家

payoffs:

• 如果获胜了，那么会得到奖品B
• 代价是C，并且假设B==2C
• 有一个附加成本，如果你的坐标是x，winner 坐标为y，你会付出成本-$\left | x-y\right |$

e.g.

1. x如果赢了, payoffs = B-C
2. x参与了，但是y赢了比赛，payoffs = $-c-\left | x-y\right |$
3. x不参与,y赢得了比赛，payoffs = $\left | x-y\right |$

纳什均衡点分析：

如果参选人是奇数，那么最中间的那个人站起来是纳什均衡点

如果参选人是偶数，那么最中间的两个人站起来是纳什均衡点

分析的本质是任何人对现在的结果都不会后悔，那么就是纳什均衡点。

那么接下来的问题是，对称的两个候选人是可能存在纳什均衡点的，那么这个区间是什么？

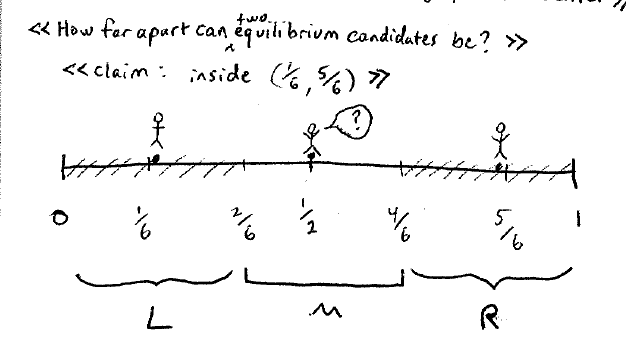
只要两边的人站起来后，最中间的那个人不会站起来（图中有？的人），那么就是纳什均衡。

因此只要对称的选举人在$[\frac{1}{6}, \frac{5}{6}]$，那么就是纳什均衡的。